Для оценки потенциальных рисков и возможных выгод опционов используют показатели чувствительности, которые принято называть греками (greeks). При использовании ванилла-опционов обращаются не только к пяти общеизвестным грекам, но и углубляются иной раз в более сложные материи, имеющие отношение к вопросам определения меры риска опционных контрактов. С бинарными (числовыми) опционами дело оценки чувствительности обстоит одновременно и сложнее, и проще.
Другие статьи мастер-класса «Бинарные опционы»
Бинарные опционы: математика все та же
Сложности связаны с тем, что математика бинарных опционов является понятной и легко считается по общеизвестным моделям лишь для европейских опционов. Однако европейские бинары являются менее интересными с точки зрения инвестиционной привлекательности по сравнению с американскими бинарными опционами. Причина очевидна, — американский бинар будет исполнен в тот же миг, как только базовый актив достигнет барьера (цены страйк). В то время, как держатели европейских бинаров при тех же самых обстоятельствах должны оставаться в позиции до истечения опциона, если они намерены получить максимальную стоимость выплат по контракту.
При этом модели оценки стоимости американских бинаров хотя и существуют, но достаточно сложны и для понимания, и для использования их в расчётных задачах. Кроме того, изыскания в области решения задачи вычисления цены (и греков) бинарных опционов еще не привели к получению однозначно приемлемой модели. Сложности добавляет также и то, что на практике банки часто пользуются собственными разработками, которые обычно являются закрытыми.
Самый важный грек бинаров — дельта
Вместе с тем, есть и хорошая новость. На самом деле для бинарных опционов почти все основные показатели чувствительности (гамма, тэта, вега, ро) являются малосущественными. Во всяком случае, их воздействие на цену опциона настолько мало по сравнению с дельтой, что использование греков становится бессмысленными. Во всяком случае, в том объеме, как это практикуется с ванилла-опционами. Исключение составляют случаи управления крупными опционными портфелями, с которыми индивидуальные инвесторы обычно дела не имеют.
Профиль дельты бинаров идентичен гамме ванилла-опционов с тем же страйком, что и барьер бинарного опциона (см. рис. 1), просто потому, что профиль доходности бинарного опциона является дельтой соответствующего ванилла-опциона (с тем же страйком, что и барьер). А поскольку гамма ванилла-опциона является частной производной от дельты по базовому активу, то получается данная идентичность (дельта бинара = гамма ванилла-опциона).
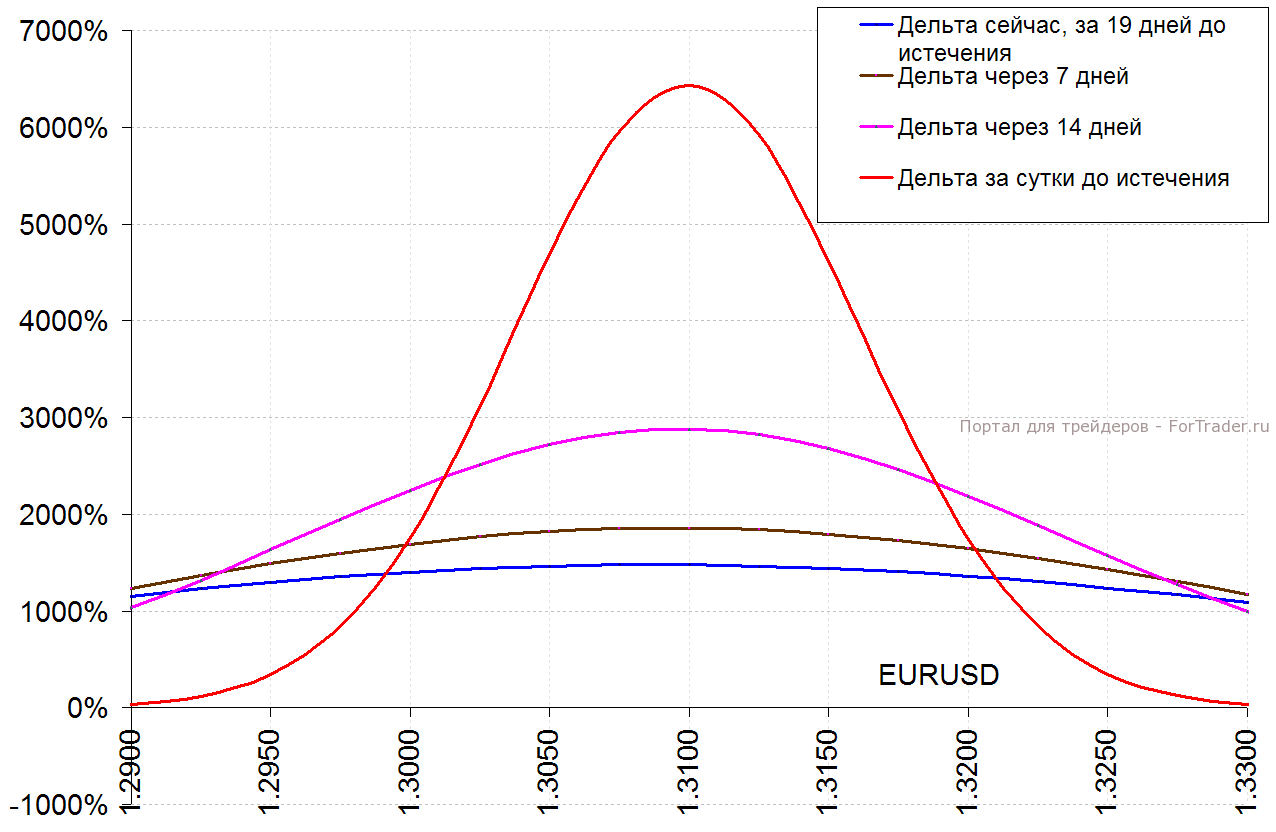
Профиль американского бинара (скажем, касательного, или одно касание) имеет ту же форму с несколько большей экспрессией в приближении к цене исполнения опциона (1.31 из примера выше). Причем, разумеется, при любом сроке до истечения профиль «американца» будет стремиться к дельте европейского бинара на дату истечения опциона (красная линия на рис. 1). Естественно также, что правой части дельты у американского бинара (выше цены страйк) просто не будет, поскольку по достижении барьера этот опцион будет немедленно исполнен (см. рис. 2).
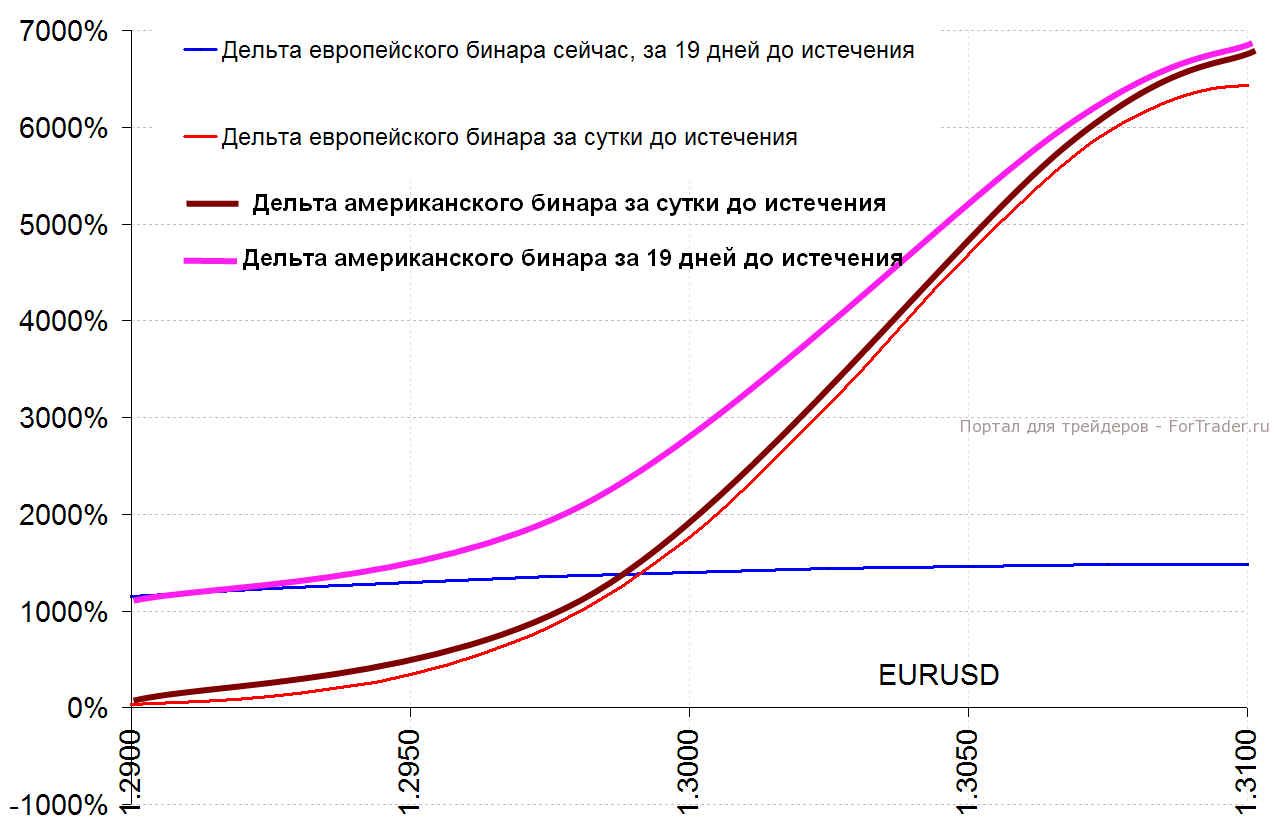
Причем заключительный отрезок пути к барьеру для американского бинара точно рассчитать чрезвычайно сложно. Да и ненужно. Поскольку в непосредственной близости от барьера маркет-мейкеры предпочитают закрывать торговлю опционами (во всяком случае, так поступает Saxo Bank). Поэтому, если ваш бинар находится в нескольких пунктах от барьера, то при всём желании позицию вы не закроете. Либо надо надеяться на исполнение опциона, либо ждать отката от уровня барьера.
Конечно, иногда имеет смысл учитывать также и тэту (чувствительность к времени до истечения), и вегу (чувствительность по волатильности). Однако следует заметить: волатильность опциона непосредственно влияет на вероятность достижения барьера, который мы, собственно говоря, и торгуем опционом. Поэтому, как говорится, всё уже в ценах.
В отношении тэты также можно сказать, что её значение для торговца бинаром имеет весьма малое значение, если речь идет о простой спекуляции. Значительно более важную роль играет другое обстоятельство. А именно, сумели ли мы угадать для отрезка времени, на котором опцион будет жив, достигнет базовый актив барьера бинара, или же нет.
Михаил Чекулаев, автор книги «Финансовые опционы» при поддержке Saxo Bank