Квадратурные индикаторы RAOS и RAOSQ – больше информации для торговой стратегии

Настоящая публикация является продолжением ранее опубликованной статьи Цифровая обработка торговых сигналов для торговой стратегии.

В ранее опубликованной статье отмечено:

котировочный сигнал в среднем состоит из множества ритмов с различными периодами и размахами (амплитудами), наложенных друг на друга, при этом ритмы непостоянные – возникают и исчезают в ходе своей эволюции во времени,
при возможности отделять эти ритмы друг от друга и по их соотношению между собой, можно принимать торговые решения, то есть формировать торговые сигналы,
для разделения (расслоения) сложного котировочного сигнала на более простые компоненты (ритмы с различными периодами и различными
размахами по амплитуде) можно использовать цифровые фильтры, например цифровые фильтры нижних частот (ФНЧ),
задача ФНЧ — сгладить (усреднить) все колебания с периодами меньше задаваемого периода усреднения и оставить (пропустить) все колебания с периодами больше задаваемого периода усреднения. При этом возможно гибко изменять соотношение между собой пропускаемых (не сглаживаемых) ритмов (то есть, изменять нужным образом реакцию сглаженной кривой на выходе ФНЧ (индикатора) на изменение котировочного сигнала во времени).

Отметим, что функция изменения соотношения между собой пропускаемых (не сглаживаемых) ритмов называется частотной характеристикой цифрового фильтра (цифрового индикатора). Формируя требуемую частотную характеристику можно получить индикатор с нужной реакцией на изменение котировочного сигнала.

Торговая стратегия с использованием индикаторов RAOS и RAOSQ

Построение торговой стратегии и формирования торговых сигналов с использованием квадратурных цифровых индикаторов RAOS и RAOSQ основано именно на разделении (расслоении) сложного котировочного сигнала на более простые компоненты (ритмы с различными периодами и различными размахами по амплитуде). Индикаторы RAOS и RAOSQ совместно достаточно детально отражают динамику этих ритмов.

Термин «цифровые» обозначает, что индикаторы являются цифровыми фильтрами. А термин «квадратурные» обозначает, что индикаторы применяются в паре, и их взаимное динамическое изменение во времени по отношению друг к другу происходит в квадратуре, например, взаимное динамическое изменение во времени математических функций SIN и COS по отношению друг к другу, также происходит в квадратуре.

В настоящее время для проектирования алгоритмов индикаторов RAOS и RAOSQ требуется специальное ПО для расчета (синтеза) цифровых фильтров. По различным методикам расчёта (синтеза) в настоящее время имеется обширная литература. Полученные алгоритмы работы индикаторов RAOS и RAOSQ выполняются последовательно в реальном времени, то есть они не перерисовываются.

Результаты работы индикаторов RAOS и RAOSQ

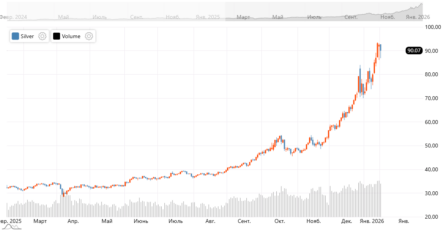
На рисунке 1 изображена скользящая средняя RAMA с периодом сглаживания 20 (красная линия) (подробнее об индикаторе смотри в статье «Улучшенная модификация скользящей средней – индикатор RAMA против SMA»), также изображен индикатор RAOS(20) (сплошная и пунктирная черные линии), согласованный по своей частотной характеристике (при проектировании) со скользящей средней RAMA(20). Частотная характеристика подбиралась так, чтобы RAOS отражал скорость изменения RAMA.

Из рисунка 1 видно, если линия индикатора RAOS(20) выше линии индикатора RAMA (20), то линия индикатора RAMA (20) двигается «вверх», если линия индикатора RAOS(20) ниже линии RAMA (20), то линия индикатора RAMA (20) двигается «вниз».

Индикатор RAOS отображается в поле котировок в абсолютных единицах относительно линии скользящей средней RAMA, а не в сноске «внизу» относительно нулевой линии. Также, индикатор RAOS взаимодействует с котировочным сигналом как опорная линия.

Индикатор RAOS характеризует величину скорости (первой производной) изменения линии скользящей средней RAMA, с которой он согласован по своей частотной характеристике.

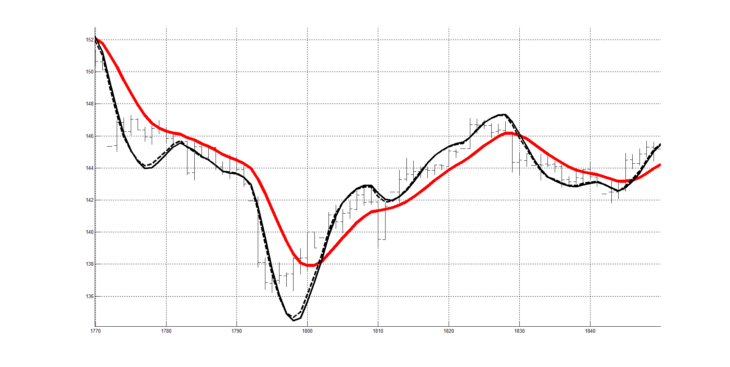
Рис. 1. Скользящая средняя RAMA(20) с периодом сглаживания 20 (красная линия) и индикатор RAOS(20) (сплошная и пунктирная черные линии), согласованный по своей частотной характеристике со скользящей средней RAMA(20).

На рисунке 2 изображена скользящая средняя RAMA (20) с периодом сглаживания 20 (красная линия), также изображен индикатор RAOSQ (20) (сплошная и пунктирная красные линии). Индикатор RAOSQ (20) является квадратурой по отношению к индикатору RAOS(20). В данном случае, если индикатор RAOS отражает скорость (первую производную) изменения линии скользящей средней RAMA, то квадратурный индикатор RAOSQ отражает ускорение (вторую производную) изменения линии скользящей средней RAMA. То есть, частотная характеристика (при проектировании) индикатора RAOSQ подбиралась так, чтобы индикатор RAOSQ отражал ускорение изменения скользящей средней RAMA

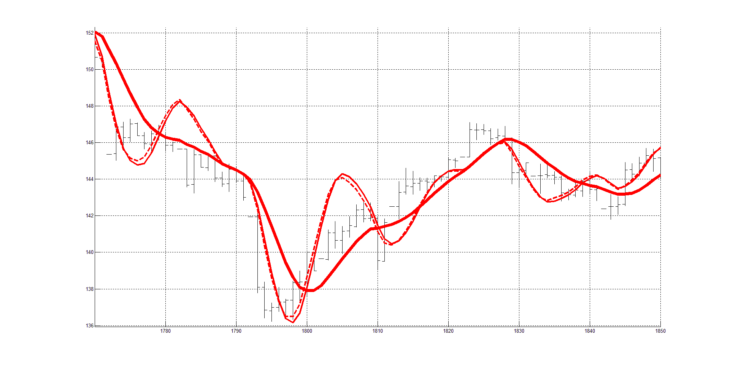
Рис. 2. Скользящая средняя RAMA(20) с периодом сглаживания 20 (красная линия) и индикатор RAOSQ(20) (сплошная и пунктирная красные линии), согласованный по своей частотной характеристике со скользящей средней RAMA(20).

Из рисунка 2 видно, что квадратурный индикатор RAOSQ располагается относительно линии скользящей средней RAMA в соответствии с изменением темпа прироста (или замедления) изменения линии скользящей средней RAMA.

Также видно, что если движение «вниз» линии скользящей средней RAMA замедляется, то индикатор RAOSQ переходит в положение «выше» линии скользящей средней RAMA, и наоборот, если движение «вверх» линии скользящей средней RAMA замедляется, то индикатор RAOSQ переходит в положение «ниже» линии скользящей средней RAMA.

Индикатор RAOSQ характеризует величину ускорения (или замедления) (то есть, второй производной) изменения линии скользящей средней RAMA, с которой он согласован по своей частотной характеристике.

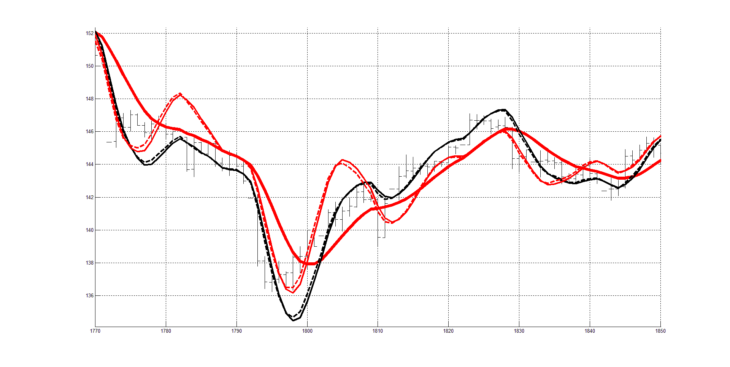
На рисунке 3 совмещены рисунки 1 и 2. Из него видно, что совместно квадратурные индикаторы RAOS и RAOSQ достаточно полно описывают динамику изменения скользящей средней RAMA.

Возможно определение «разворотов» линии скользящей средней RAMA или «возобновлений» продолжения направленного движения линии скользящей средней RAMA.

Индикатор RAOSQ более “реактивный”, чем индикатор RAOS, то есть реагирует с “упреждением” на динамические изменения в динамике линии скользящей средней RAMA, с которой он согласован по своей частотной характеристике, то есть даёт дополнительную информацию для более точного определения “разворотов” и “ продолжений ”.

Индикаторы RAOS и RAOSQ можно считать осцилляторами, если рассматривать их как изменяющиеся (осциллирующие) относительно линии, согласованной с ними скользящей средней RAMA.

Рис. 3. Результат совмещения рисунков 1 и 2.

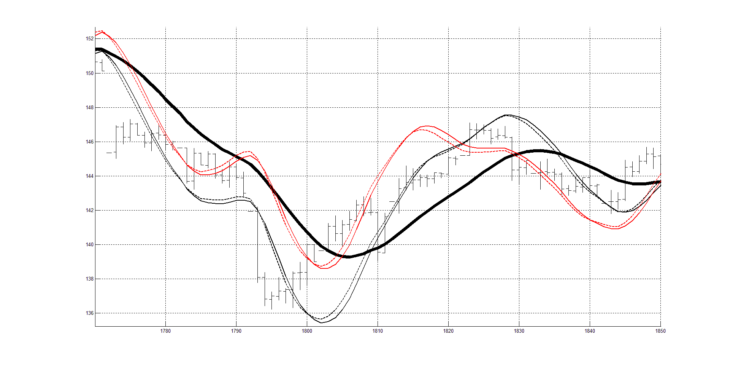
Рис. 4. Скользящая средняя RAMA с периодом сглаживания 40 (чёрная линия), также изображены квадратурные индикаторы RAOS (40) (сплошная и пунктирная черные линии), RAOSQ (40) (сплошная и пунктирная красные линии), согласованные по своей частотной характеристике со скользящей средней RAMA(40).

Двухпериодная и трёхпериодная системы технического анализа

На рисунке 5 совмещены рисунки 3 и 4 и изображена двухпериодная (20 и 40) система технического анализа с использованием двух скользящих средних RAMA (20), RAMA (40) и согласованных с ними двух пар цифровых квадратурных индикаторов RAOS (20), RAOSQ (20), RAOS (40), RAOSQ (40). По совместной динамике линий индикаторов возможно формировать торговые сигналы.

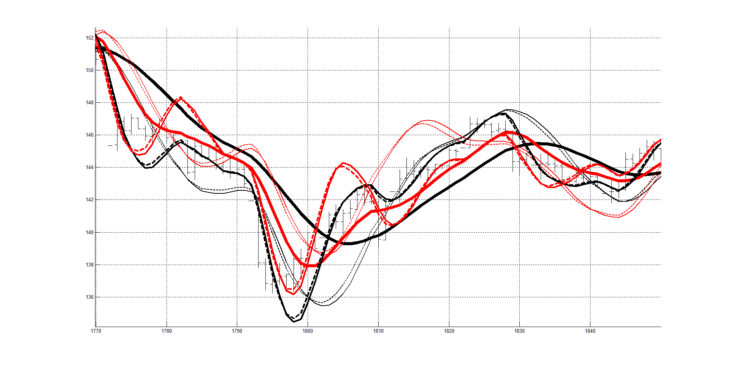
Рис. 5. Результат совмещения рисунков 3 и 4. Двухпериодная (20 и 40) система технического анализа.

Далее, на рисунках 6 и 7 полученная двухпериодная система технического анализа (рисунок 5) изображена для других участков котировочного сигнала.

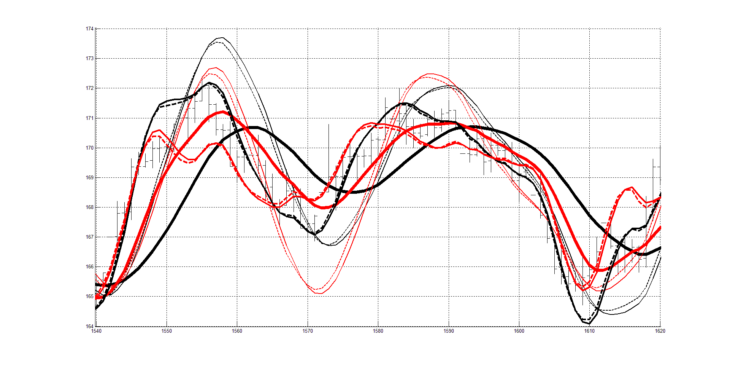
Рис. 6. Двухпериодная (периоды 20 и 40) система технического анализа, второй участок котировок.

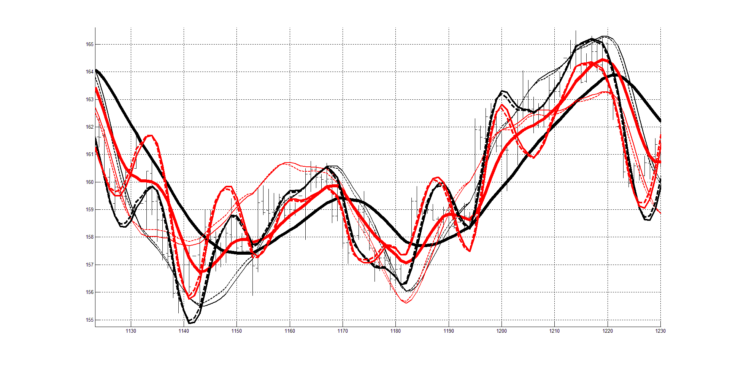
Рис. 7. Двухпериодная (периоды 20 и 40) система технического анализа, третий участок котировок.

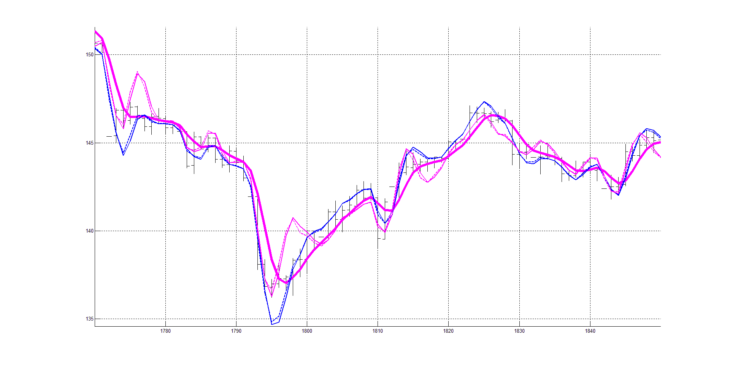
Рис. 8. Скользящая средняя RAMA с периодом сглаживания 9, квадратурные индикаторы RAOS(9) и RAOSQ(9) (синий цвет – линии индикатора RAOS(9)), согласованные по своей частотной характеристике со скользящей средней RAMA(9).

На рисунке 9 совмещены рисунки 3 и 8.

На рисунке 9 изображена двухпериодная (периоды 9 и 20) система технического анализа с использованием двух скользящих средних RAMA (9), RAMA (20) и согласованных с ними двух пар цифровых квадратурных индикаторов RAOS (9), RAOSQ (9), RAOS (20), RAOSQ (20).

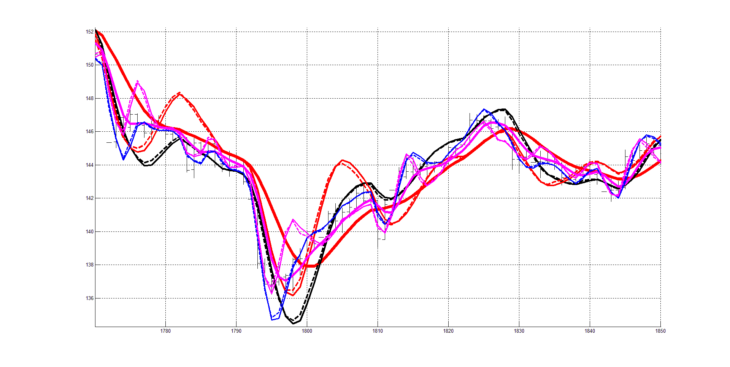
Рис. 9. Результат совмещения рисунков 3 и 8. Двухпериодная (периоды 9 и 20) система технического анализа.

На рисунке 10 совмещены рисунки 4 и 9.

На рисунке 10 изображена трёхпериодная (периоды 9, 20 и 40) система технического анализа с использованием трёх скользящих средних RAMA (9), RAMA (20), RAMA (40) и согласованных с ними трёх пар цифровых квадратурных индикаторов RAOS (9), RAOSQ (9), RAOS (20), RAOSQ (20), RAOS (40), RAOSQ (40).

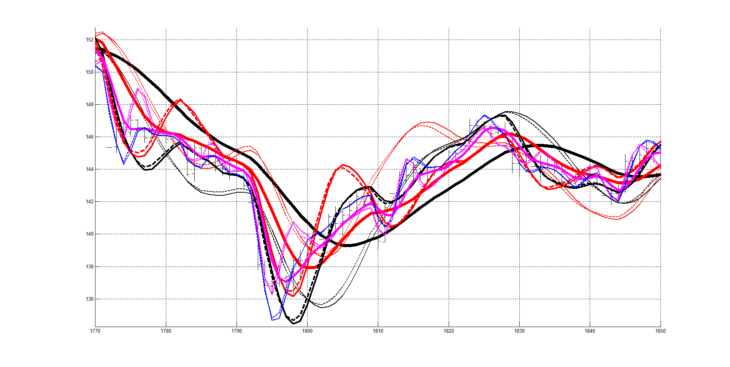
Рис. 10. Результат совмещения рисунков 4 и 9. Трёхпериодная (периоды 9, 20 и 40) система технического анализа.

На рисунках 11. 12 изображена трехпериодная система технического анализа c периодами 9, 20, 40 для других участков котировочного сигнала.

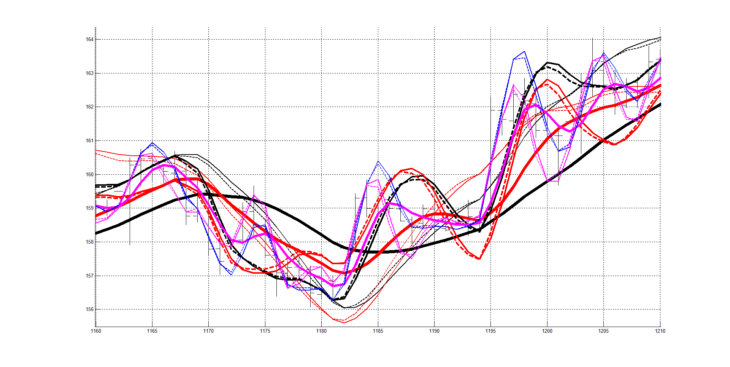
Рис. 11. Трёхпериодная (периоды 9, 20 и 40) система технического анализа, второй участок котировок.

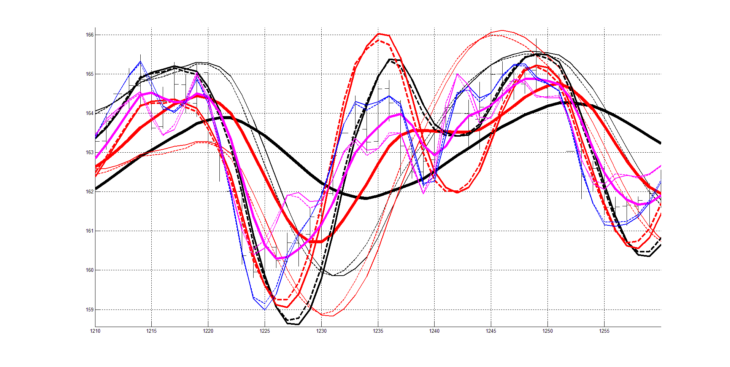
Рис. 12. Трёхпериодная (периоды 9, 20 и 40) система технического анализа, третий участок котировок.

Рассмотренная многопериодная система технического анализа строится из заданного числа скользящих средних RAMA с заданными периодами сглаживания. При этом каждая скользящая средняя RAMA, настроенная на свой период сглаживания сопровождается парой квадратурных индикаторов RAOS и RAOSQ , согласованных с ней по своей частотной характеристике.

Тройка согласованных индикаторов (RAMA, RAOS, RAOSQ, (скользящая средняя, её скорость и ускорение)) считается базовым компонентом при построении многопериодной системы технического анализа.

Совместно квадратурные индикаторы RAOS и RAOSQ достаточно полно отражают динамику изменения линии скользящей средней RAMA. Индикатор RAOS отражает скорость изменения (первую производную) линии во времени скользящей средней RAMA, индикатор RAOSQ отражает ускорение изменения (вторую производную) линии во времени скользящей средней RAMA.